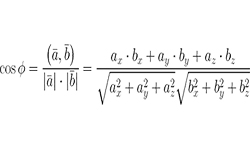Скалярное произведение векторов

Отрезок прямой, имеющий численное значение и направление, называется вектором, обозначается латинской буквой со стрелкой сверху. Над векторами можно совершать различные линейные операции, в том числе умножение. Помимо умножения векторов на числа, вектора можно перемножать друг с другом. Произведение длин векторов на косинус угла между ними называется скалярным произведением векторов.

В результате перемножения двух векторов получаем положительное или отрицательное число (скаляр). Знак зависит лишь от значения косинуса, т.к. длина ненулевого вектора всегда величина положительная.
Скалярное произведение можно записать через координаты векторов а и b. Скалярное произведение векторов равняется сумме попарных произведений соответствующих координат этих векторов.
На плоскости.
Пусть координаты векторов: a = {a_x ; a_y} и b = {b_x ; b_y}, тогда скалярное произведение определяем по формуле:

В пространстве.
Пусть векторы а и b заданы координатами: a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z}, вычисляем скалярное произведение векторов:

Скалярное произведение n — мерных векторов определяем по формуле:

где a = {a₁ ; a₂ ; ... ; a_n} и b = {b₁ ; b₂ ; ... ; b_n}

Свойства скалярного произведения векторов:
1. скалярное произведение вектора на себя равно квадрату его модуля и всегда будет больше или равно нулю.
2. скалярное произведение нулевого вектора на себя равно нулю.
3. a · b = b · a — коммуникативный или переместительный закон скалярного произведения.
4. скалярное произведение не нулевых векторов равняется нулю, если векторы ортогональны.
5. (аa) · b = а(a · b) — константу можно вынести из скалярного произведения.
6. (a + b) · c = a · c + b · c — скобки можно раскрывать.
Кроме скалярного произведения существует векторное произведение. В этом случае результатом перемножения двух векторов является вектор.