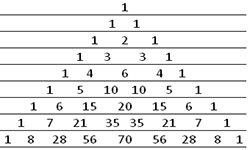
Известно, что натуральные числа, исключая 1, делятся на простые и составные. Елиница (1) ни к простым, ни к составным числам не относится, т. к. имеет лишь один делитель — 1. Натуральное число (большее 0), у которого имеется лишь два разных делителя: оно само и 1, является простым числом. Возьмем числа 2, 3, 5, 19, 1979. Эти числа делятся нацело только на себя и на 1, следовательно, мы имеем дело с простыми числами. Остальные числа считаются составными. Например, 4, 10, 144. Простых чисел, в то же время как и составных, бесконечно много. Выдающийся древнегреческий математик Евклид, проживавший в третьем веке до н. э. дает такое определение простым числам: «Простое число есть измеряемое только единицей ...». В «Началах» Евклид приводит доказательство бесконечного множества простых чисел. Допустим, что у простых чисел имеется конечное число. Если их перемножить и прибавить единицу, то получим число, которое мы не сможем поделить без остатка на любое из этого набора простых чисел. В остатке всегда остается 1. Отсюда выходит, что должно быть простое число, не вошедшее в этот набор, на которое делится полученное число, что является противоречием. Факт бесконечности простых чисел был доказан и другими математиками в разные времена. Из известных науке простых чисел наибольшее — число Мерсенна, равное 2 в степени 132049 — 1. Вопрос о том, как простые числа распределены в натуральном ряду, очень сложный. Есть участки в натуральном ряду, где они расположены гуще и даже очень близко друг к другу. Возьмем к примеру, 2 и 3, 191 и 193. Такие пары простых чисел называют близнецами.
Чтобы быстро и правильно определить, относится ли заданное число к простым, воспользуйтесь онлайн калькулятором.