Образуют ли вектора базис

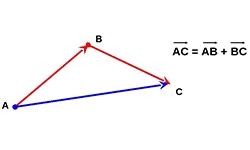
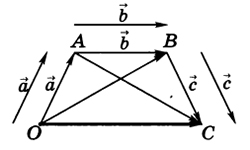
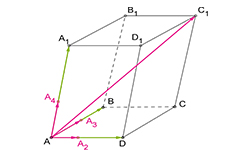
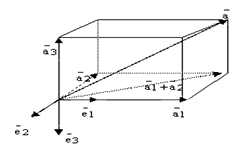
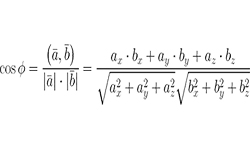Базисом пространства является система векторов, в которой остальные векторы пространства легко можно записать в виде линейной комбинации векторов, которые входят в базис. На практике базис проверяют, как правило, на плоскости или в пространстве.
Чтобы узнать, образуют ли вектора а₁, а₂, а₃ базис трехмерного пространства и определить координаты вектора b в этом пространстве, необходимо из координат этих векторов составить определитель матрицы третьего порядка. Если определитель не равняется нулю, вектора образуют базис, соответственно, вектор b раскладывается по данному базису. При нулевом определителе вектора а₁, а₂, а₃ не являются базисными и вектор b нельзя разложить по данному базису.
Линейная независимость векторов является условием образования базиса.

Онлайн калькулятор поможет вам проверить, образует ли система векторов базис. Для этого необходимо ввести координаты заданных векторов, указать размерность пространства (от 2 до 6). В n-мерном пространстве через n заданных векторов можно выразить другие вектора пространства. Важно правильно выбрать базис.

Размерность пространства векторов:			23456
Введите значения векторов:
a1 = {	;	;	}
a2 = {	;	;	}
a3 = {	;	;	}