Числа Фибоначчи

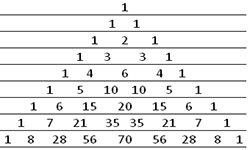
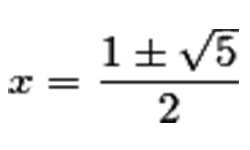Имя Леонардо Фибоначчи, автора «Книги об абаке» (1202 г.), хранившей много веков основные сведения по алгебре и арифметике, сегодня чаще всего связывают с выведенной им числовой последовательностью: 1,1,2,3,5,8,13,21,34,55,89,144 ... и названной в его честь — Числа Фибоначчи. Впрочем, коэффициенты ряда были известны и использовались еще ранее в древней Индии. Сегодня числа Фибоначчи широко используются в экономике, биологии, программировании, в сфере финансов. Они представляют такую последовательность, в которой каждое последующее число равно сумме двух предыдущих до него чисел. Они встречаются в разных числовых, комбинаторных, геометрических ситуациях, в различных областях жизни, в живой природе. Эти числа в различных спиральных формах можно найти в мире растений, например, семечки подсолнуха, ячейки у ананаса, чешуйки у еловой шишки размещены спиралями, при этом, их количество являются числами Фибоначчи. В арифметике Чисел Фибоначчи наблюдается немало интересного, например, каждое 3-е число Фибоначчи — четное, всякое 4-е — делится на 3, нулем оканчивается каждое 15-е. При возрастании чисел в последовательности они становятся все ближе к золотому сечению. Рассчитать число Фибоначчи можно по формуле: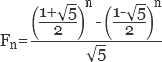Быстро произвести вычисление чисел Фибоначчи можно с помощью онлайн-калькулятора. Для этого вам нужно ввести n-ый член, для которого требуется рассчитать ряд Фибоначчи, в окошко “расчеты” и нажать кнопку «Вычислить». Искомые числа Фибоначчи практически сразу же появятся в окне “последовательность чисел”.

Вычисление чисел Фибоначчи онлайн