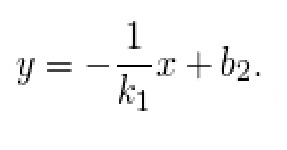Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
Тригонометрические функции в прямоугольном треугольнике.
Пусть дан прямоугольный треугольник АВС с гипотенузой с, катетом а — противолежащим углу β, катетом b — прилежащим к углу β. Гипотенуза © — самая длинная сторона треугольника, лежащая против прямого угла. Сумма всех углов треугольника, лежащего на плоскости, равна «пи» (180°), сумма углов прямоугольного треугольника между катетами и гипотенузой лежит между 0 и 90°.
Найдем тригонометрические функции произвольного угла α.
Отношение противолежащего катета а к гипотенузе с будет синусом угла (α) sin α = а/с
Отношение прилежащего угла b к гипотенузе с — косинус угла cos α = b/с
Отношение противолежащего катета а к прилежащему b — тангенс угла tg α = а/b
Отношение прилежащего катета b к противолежащему а — котангенс угла ctg α = b/а
Отношение гипотенузы с к прилежащему катету b — секанс угла sec α = с/b
Отношение гипотенузы с к противолежащему катету а — косеканс угла cosec α = с/а
Определение тригонометрических функций с помощью единичного круга.
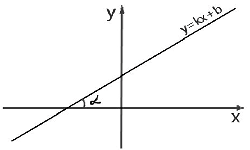
В прямоугольной системе координат с началом в точке О и осями Ох и Оу возьмем окружность радиусом, равным единице (r = 1), с центром в точке О. Отметим на окружности точку М (х,у). Угол, заключенный между радиус-вектором ОМ и положительным направлением оси Ох, равняется а.
Отношение ординаты у точки М (х,у) к радиусу r называется синусом угла (α): sin α = y/r.
При r = 1 синус равняется ординате точки М (х,у).
Отношение абсциссы х точки М (х,у) к радиусу r — косинус угла (α): cos α = x/r.
Отношение ординаты у к абсциссе х точки М (х,у) — тангенс угла (α): tan α = y/x (х не равняется 0).
Отношение абсциссы х у ординате у точки М (х,у) — котангенс угла (α): cot α = x/y (у не равняется 0).
Отношение радиуса r к абсциссе х точки М (х,у) — секанс угла (α): sec α = r/x = 1/x (при r = 1; х не равно 0).
отношение радиуса r к ординате у точки М (х,у) — косеканс угла (α): csc α = r/y = 1/y (при r = 1; y не равно 0).
Это — простейшие тригонометрические функции. Каждому углу соответствуют свои тригонометрические функции. Если известен sin, cos, tg или ctg, можно найти угол. Зная величину угла, можно вычислить соотношение сторон. С помощью онлайн калькулятора тригонометрических функций вы легко найдете требуемую величину. Вам необходимо лишь ввести первоначальные данные.
