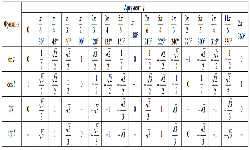
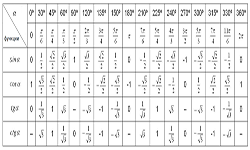
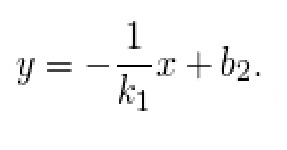Для построения графика линейной функции или определения координат точек пересечения прямой с осью Ох и Оy важно уметь находить угол наклона прямой.
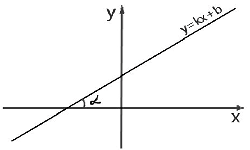
Углом наклона прямой к оси Ох является угол, который считают против часовой стрелки от положительного направления Ох к прямой.
В уравнении y = kх + b, где b — координата «у» — точки пересечения прямой с Оy, коэффициент k при х — коэффициент наклона прямой.
Этот коэффициент равняется тангенсу угла а, образованного между прямой и положительным направлением оси Ох: k = tg а.
Если прямая наклонена вправо, то угол, образованный между прямой и осью Ох, будет острым, тангенс угла (tgа) и коэффициент наклона k больше нуля. Угол определяем по формуле: a = arctg k.
Если наклон прямой влево, то угол между прямой и осью Ох будет тупым, а тангенс угла (tgа) и коэффициент k меньше нуля. Угол a = Пи — arctg |k|.
Угол наклона равняется 0, если прямая расположена параллельно Ох или совпадает с ней.
Зная координаты 2-х точек, расположенных на прямой, можно легко рассчитать угол наклона как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между ними.
Пусть координаты первой точки (х1,y1), координаты второй (х2,y2), тогда угловой коэффициент будет равняться: (y2 — y1): (х2 — х1),
где (y2 — y1) — величина изменения координаты «у», (х2 — х1) — изменение координаты «х». Из полученной величины возьмем арктангенс и определим угол наклона прямой.
Быстро определить угол наклона прямой, вам поможет онлайн калькулятор.