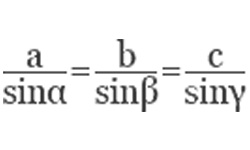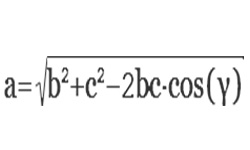Теорема Пифагора — главное утверждение геометрии. Так звучит ее формулировка : площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
S = S1 + S2
Несмотря на то, что теорема названа именем знаменитого математика и философа Пифагора, проживавшего в Древней Греции в VI в. до н. э., уже давно установлено, что подобное утверждение было известно намного раньше. Пифагор же открыл доказательство теоремы, которая сначала определяла отношение между площадями квадратов, которые были построены на катетах и гипотенузе вероятно равнобедренного прямоугольного треугольника. Сегодня известны десятки разных доказательств Пифагоровой теоремы, которая лежит в основе множества геометрических вычислений. Вторая формулировка теоремы, алгебраическая, читается как: квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов его катетов, что можно выразить формулой:
c2 = a2 + b2
В данной формуле:
а, в — величины катетов;
с — величина гипотенузы.
Если нужно найти гипотенузу, необходимо вычислить сумму квадратов катетов, а затем извлечь из нее корень квадратный. По формуле:
c2=a2+b2
c=√a2+b2
Если нужно найти величину катета, из квадрата гипотенузы вычитаем квадрат другого катета. Из полученного результаты извлекаем корень квадратный.
a=√c2-b2
Сформулирована обратная теорема Пифагора:
если квадрат одной стороны рассматриваемого треугольника равен сумме квадратов остальных двух сторон, то он считается прямоугольным.
Быстро и правильно произвести математические расчеты вам поможет онлайн калькулятор, вам надо только подставить исходные данные.
