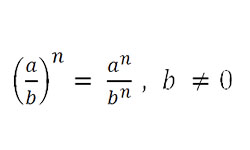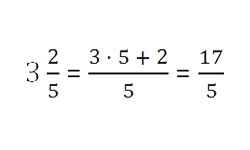Рассмотрим разные варианты:
а) сложение с одинаковыми знаменателями.
При выполнении действия сложения дробей, имеющих одинаковые знаменатели, нужно сложить числители исходных дробей, при этом знаменатель оставить прежний, равный знаменателю обеих дробей:
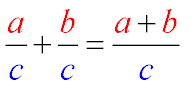
а — величина числителя 1-й дроби;
b — величина второго числителя;
с — знаменатель дробей.
б) сложение с разными знаменателями.
Чтобы выполнить действие сложения дробей с разными знаменателями, следует:
1. привести дроби к одному общему знаменателю, рассчитав наименьшее общее кратное;
2. сложить дроби, как в случае с дробями с одинаковые знаменатели, т. е числители дробей складываются, а знаменатель — без изменений.
3. если у вновь полученной дроби имеются общие множители, ее надо сократить. В противном случае пример считается неоконченным;
4. неправильную дробь следует преобразовать в смешанную.
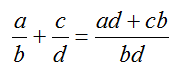
в) дроби и целого числа.
Для сложения дроби и целого числа необходимо:
1. целое число преобразовать в дробь со знаменателем которой будет 1;
2. приводим к общему знаменателю;
3. складываем дроби;
4. вновь полученную дробь, если возможно, сокращаем;
5. если в результате сложения имеем неправильную дробь, выделяем целую часть.
г) сложение смешанных дробей.
Чтобы выполнить это действие, необходимо:
1. отдельно произвести сложение целых частей;
2. отдельно — дробных частей, приведя их в случае необходимости к НОК;
3. если в дробной части вышла неправильная дробь, требуется выделить из нее целую часть и сложить с полученной целой частью.
Сложение смешанных дробей можно выразить формулой:
А, В — целые части дробей;
а, b — числители дробных частей;
с — знаменатель дроби.
С помощью онлайн калькулятора можно легко и быстро осуществить все необходимые расчеты.
Калькулятор для сложения дробей онлайн
|
|
||||
|
|
|
|||
