Радиус шара

Отрезок, соединяющий центр шара с любой точкой на его поверхности, является радиусом шара, обозначается как r или R. В зависимости от исходных данных радиус шара можно вычислить:

— по диаметру. Как известно, радиус шара равен половине его диаметра:

г = D/2,

где г — радиус, D — диаметр шара.

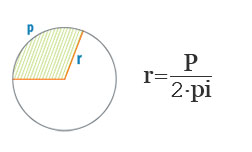
— по длине окружности.
Длина окружности © равна произведению пи на диаметр (D), через радиус шара — удвоенному произведению пи на радиус ^®:

C = πD = 2πr

Отсюда, радиус равен частному от деления длины окружности © на 2 пи:

r = С / 2π

π — величина постоянная, равна отношению длины окружности к диаметру. Число Пи, равное 3,141592653... обычно округляется до 3,14.

— по площади шара.
Площадь шара равна произведению четырех пи на квадрат радиуса:

S=4πr²,

где S — площадь шара, r — радиус.
Из этой формулы выводим форму радиуса:

r = √S / 4π,

т.е. радиус равен корню квадратному из площади шара деленной на четыре пи.

— по объему шара.
Объем шара равен произведению четырех третьих на число пи и на радиус шара в кубе:

V = 4/3 πr³,

где V — объем, r — радиус шара.
Отсюда, радиус шара равен корню кубическому из объема шара деленного на три четвертых Пи:

r = ∛(V / (¾π))

Рассчитать радиус шара через объем