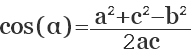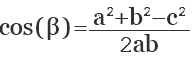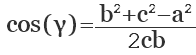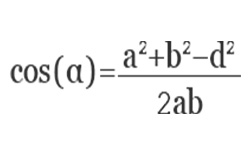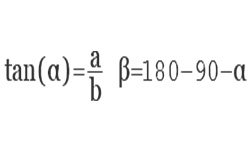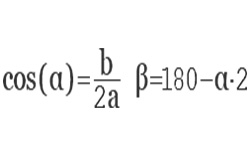Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.
α = 180°-β-γ
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), минус удвоенное произведение этих сторон (b,с) на косинус угла.
a2 = b2 + c2 — 2bc cos (α)
Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:
cos (α) = (b2 + c2 — a2) / 2bc
,
где а, b, с — стороны треугольника.
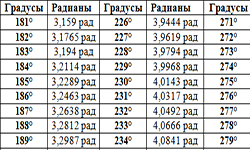
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.