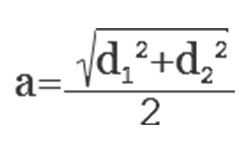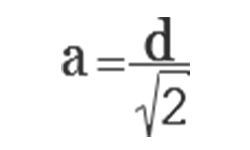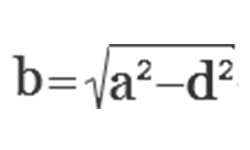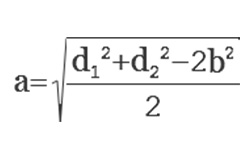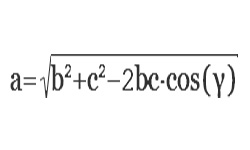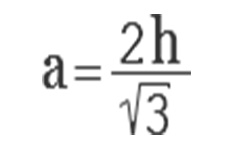Треугольник, у которого один угол прямой, называется прямоугольным. Сторона, расположенная напротив прямого угла, является гипотенузой, она самая длинная в прямоугольном треугольнике. Остальные две его стороны, образующие прямой угол — катеты. Зная величину обоих катетов, можно вычислить размер гипотенузы по теореме Пифагора:
c2 = a2+b2 ,
где a, b — катеты, с — гипотенуза прямоугольного треугольника.
Отсюда, длина гипотенузы равна корню квадратному из суммы квадратов катетов:
![]()
Калькулятор расчета длины стороны прямоугольного треугольника зная катеты
Калькулятор расчета длины стороны прямоугольного треугольника зная катет и гипотенузу
Если известна величина катета и гипотенузы и необходимо найти длину второго катета, преобразуем представленную выше формулу. В результате получаем: квадрат искомого катета будет равен квадрату гипотенузы минус квадрат другого катета. Отсюда, длина катета равна корню квадратному из разности квадрата гипотенузы и квадрата другого катета:
![]()
После того, как найдены все стороны треугольника, находим его периметр, как сумму двух катетов и гипотенузы. Площадь треугольника равняется половине произведения катетов.