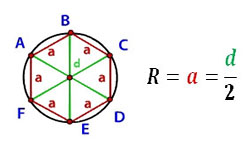
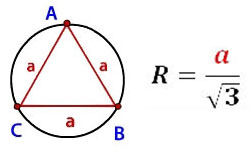
Как известно, многоугольник считается правильным, если его стороны и углы равны. Окружность называется описанной возле правильного многоугольника, если соблюдается условие, что вершины правильного многоугольника расположены на этой окружности. Центры правильного многоугольника и описанной вокруг него окружности совпадают. Отрезок, соединяющий вершину многоугольника с центром, является радиусом многоугольника и описанной вокруг него окружности.
Если известна величина стороны многоугольника и их количество, радиус описанной окружности равняется частному от деления стороны многоугольника (a) на 2 sin 360° деленное на 2 n. После сокращения получим формулу:
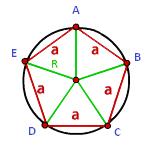
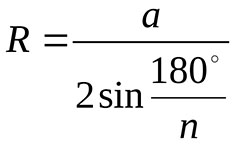
В приведенном выражении:
R — величина радиуса окружности;
a — величина стороны;
n — количество всех сторон.
Чтобы быстро и правильно определить R описанной окружности, воспользуйтесь онлайн калькулятором. Подставив в формулу исходные данные, вы тут же получите верный результат.