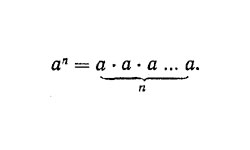Корнем арифметическим натуральной степени n из числа а (неотрицательного) считается число х, возведя которое в степень n у нас получится число а. При этом степень n>=2.
Т. е. xn=a
где х — арифметический корень (неотрицательный) из числа а n-ой степени
n — степень, показатель корня
а — неотрицательное подкоренное число
nva — обозначение корня арифметического из заданного числа а n-ой степени.
В том случае, если степень n имеет цифру 2, ее не ставят, а пишут vа. Корень 2-й степени считают квадратным, 3-й — кубическим.
Если показатель корня (n) представляет собой четное число, то можно высчитать корень n-й степени из положительного (или равного 0) числа a.
Из отрицательного числа a (меньше 0) корень четной степени отсутствует.
Если n- число нечетное, то имеется лишь один корень (из положительного, отрицательного, а также равного 0 числа) n-й степени.
В данном равенстве корень нечетной степени из числа a, имеющего отрицательное значение, записан через арифметический корень, имеющий ту же степень.
Извлекать разные корни (квадратные, кубические, 4-й степени и т.д.) из чисел можно с помощью таблицы квадратов, кубов, 4-й степени и т.д.
Воспользовавшись онлайн калькулятором корней, вы получите простое и быстрое вычисление корня любой степени.