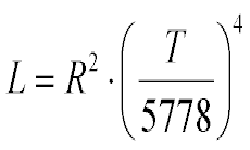Треугольник — геометрическая фигура с 3-мя сторонами и 3-мя углами. Отрезок, опущенный из вершины треугольника к противоположной ей стороне и поделивший этот угол пополам, считается биссектрисой. В треугольнике 3 вершины, соответственно, можно провести 3 биссектрисы. В зависимости от исходных данных длину биссектрисы можно рассчитать:
— через две стороны и угол, как удвоенное произведение двух сторон на косинус половины угла между ними и все это поделенное на сумму длин этих сторон: 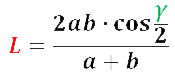
где L — биссектриса; a, b — стороны; γ — угол между сторонами а и b, который биссектриса делит пополам.
— через полупериметр и стороны, как удвоенный корень квадратный из произведения двух сторон на полупериметр и на разницу между полупериметром и третьей стороной, после чего полученный результат делится на сумму двух сторон: 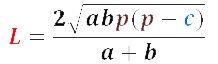
где L — биссектриса; a, b, с — стороны; p — полупериметр, равный половине суммы трех сторон треугольника p=(a+b+c)/2.
— через три стороны, как корень квадратный из произведения двух сторон на сумму трех сторон и на величину, полученную в результате вычитания из суммы двух сторон третьей стороны, затем полученный результат следует поделить на сумму двух сторон: 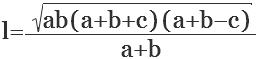
где L — биссектриса; a, b, с — стороны.
— через две стороны и отрезки третьей стороны, полученные делением биссектрисы, проведенной из угла между сторонами а и b на сторону с. В этом случае длина биссектрисы равна корню из произведения двух сторон минус произведения отрезков 3-й стороны: 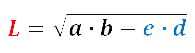
где L — биссектриса; a, b — стороны треугольника; d, e — отрезки от деления биссектрисой.