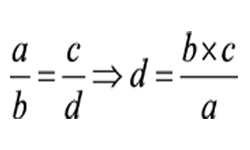Основой натурального логарифма является число е (число Эйлера) — математическая константа, равная 2.71828182845905 с пределом (1 + 1/n) n, при этом n — стремится к бесконечности. Возведение числа е в степень означает возведение в степень числа Эйлера e x = exp (x). Число е в 1-й степени, как и любое число в этой степени, будет равно самому себе, т.е. 2.71828182845905. При возведении числа Эйлера (е) в нулевую степень ответ будет равняться 1. При возведении в степень, которая будет больше единицы, ответ будет больше первоначального. Если степень будет больше нуля, но меньше 1 (например, 0,5), то ответ будет больше 1, но меньше первоначального (числа е). При возведении экспоненты в отрицательную степень нужно 1 делить на число е в заданной степени, но со знаком плюс.
Онлайн калькулятор быстро справится с возведением экспоненты в степень и выдаст точный результат.
