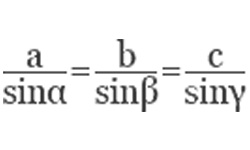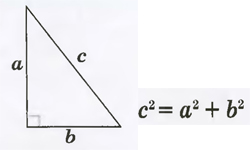Треугольник — геометрическая фигура, обладающая 3-мя сторонами и 3-мя углами между ними. Стороны обычно обозначают малыми буквами, совпадающими с обозначениями лежащих напротив вершин. Стороны данной фигуры можно вычислить несколькими способами, в зависимости от исходных данных. Так, одну из сторон треугольника можно рассчитать по теореме косинусов, если известны две другие и угол между ними. Согласно нее квадрат одной его стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: ![]() где, a, b, с — стороны, α — угол, лежащий напротив стороны а.
где, a, b, с — стороны, α — угол, лежащий напротив стороны а.
Для расчета стороны треугольника извлекаем корень квадратный из суммы квадратов других сторон минус удвоенное произведение этих сторон на cos угла между ними: ![]() Теоремой косинусов можно воспользоваться для расчета косинуса угла треугольника:
Теоремой косинусов можно воспользоваться для расчета косинуса угла треугольника: 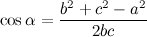 Т.е. косинус угла равен сумме квадратов двух сторон минус квадрат стороны, противолежащий углу, и все это деленное на удвоенное произведение первых двух сторон. Величину угла находим с помощью тригонометрической таблицы.
Т.е. косинус угла равен сумме квадратов двух сторон минус квадрат стороны, противолежащий углу, и все это деленное на удвоенное произведение первых двух сторон. Величину угла находим с помощью тригонометрической таблицы.
Заметим, если b2 + c2 — a2 больше 0, то угол острый; если меньше 0 — тупой; если равен 0 — прямой.
 Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач