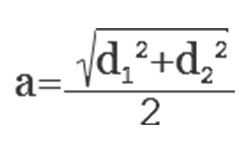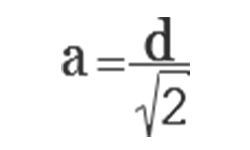Ребро куба

Куб — это четырехугольная призма, все шесть граней которой являются квадратами.

Калькулятор расчета длины ребра куба через объем
Длины трех ребер куба (длина, ширина, высота) имеют равные измерения. Объем куба равен длине ребра, возведенной в третью степень.

V = a³ ,

где Y — объем куба, а — ребро куба.
Если известен объем куба V, длину ребра (а) рассчитываем по формуле:

Калькулятор расчета длины ребра куба через диагональ
Проведенный внутри куба отрезок, соединивший вершины, расположенные на противоположных сторонах, является диагональю куба. Соединив диагональ и боковое ребро, исходящее из вершины диагонали через диагональ основания, получим прямоугольный треугольник. Его гипотенузой будет диагональ куба, а катетами — боковое ребро и диагональ основания. Через теорему Пифагора находим диагональ куба:

d = a√3 ,

где а — ребро куба, d — диагональ куба.
Если известна диагональ куба, его ребро определяем как отношение диагонали к корню из 3 по формуле:

a = d/√3 ,