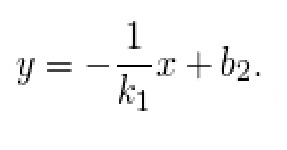При рассмотрении периодических процессов используются тригонометрические ряды. Идею представлять периодические процессы как сумму тригонометрических функций высказал Ж.Фурье. Он предложил представлять любую периодическую функцию рядом гармонически связанных синусов и косинусов — ряд Фурье.
Определение ряда Фурье
Функция f (x) имеет период Р при условии, что f (x+P)=f (x) для всех величин х. Если период функции f (x) равен 2π, рассмотрим ее поведение в интервале (-π, π).
Если функция интегрируема в данном интервале, конечным будет интеграл Дирихле:
Ряд Фурье функции f (x) можно представить в виде:
a0, an и bn — коэффициенты Фурье, которые рассчитываются по формулам:
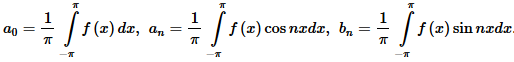
Разложение в ряд Фурье четных и нечетных функций
Ряд Фурье четной функции f (x) на отрезке (-π, π) содержит только косинусы, его можно представить в следующем виде:
где а0 и an — коэффициенты Фурье, которые можно рассчитать по формулам:
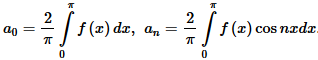
Ряд Фурье нечетной функции f (x) с периодом 2 π не содержит косинусов и раскладывается только в ряд из синусов:
коэффициенты bn можно рассчитать по формуле:
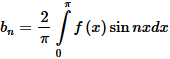
Быстро разложить функцию f (x) в ряд Фурье вам поможет онлайн калькулятор.
