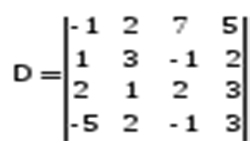
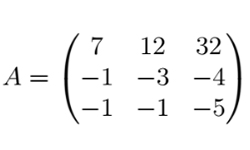Группа строк (столбцов) считаются линейно независимыми при условии, что любая из них не выражается линейно через остальные. Ранг системы строк (столбцов) матрицы — это наибольшее целое положительное число линейно независимых строк (столбцов), которое называется рангом матрицы. Он равняется наивысшему порядку ненулевого минора, обозначается Rank (A), Rang (A) или Rg (A), используется для определения возможности решения системы (совместимости системы) в принципе. Ранг нулевой матрицы независимо от размера равен нулю. Если миноры второго порядка равны 0, ранг матрицы равняется 1. Если матрица произвольных размеров имеет хоть один ненулевой элемент, ее ранг составляет не меньше единицы. В математике наиболее распространены такие способы определения ранга матрицы как способ перебора миноров, метод окаймляющих миноров, метод Гаусса, предполагающий элементарные преобразования исследуемой матрицы. Элементарные преобразования — при перестановке строк или столбцов; при умножении их на число k, отличное от нуля; при суммировании элементов строки или столбца с элементами иной строки или столбца матрицы, умноженные на k, отличное от нуля.
Воспользовавшись онлайн калькулятором, можно намного быстрее и без малейших ошибок рассчитать ранг матрицы. Для этого задаем величину строк и столбцов и вводим значение матрицы.
