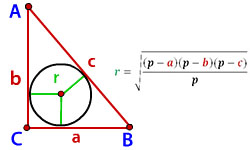
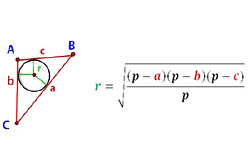
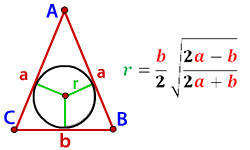
Трапецией является четырехугольник, имеющий 2 параллельные стороны. Они считаются основанием трапеции. Боковыми считаются остальные две не параллельные стороны. В трапецию несложно вписать окружность при условии равенства сумм противоположных ее сторон. Это значит, что сумма оснований трапеции равняется сумме боковых сторон. Если это условие не выполняется, окружность вписать нельзя. Вписанная окружность должна касаться всех ее сторон. В точке пересечения биссектрис трапеции находится центр вписанной окружности. Расчет радиуса производится следующим образом:
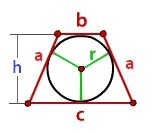
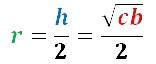
В представленной формуле:
b — величина верхнего основания;
с — нижнего;
a — величина боковых сторон;
h — длина высоты;
r — радиус.
Для определения радиуса вписанной трапеции, нужно высоту трапеции поделить на 2. Если известны величины оснований трапеции, то радиус равен половине корня квадратного из произведения его оснований.
С помощью онлайн калькулятора вы сможете быстро вычислить нужный радиус. Вам потребуется лишь подставить в формулу исходные величины.
