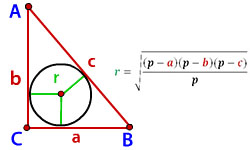
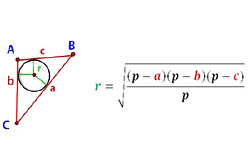
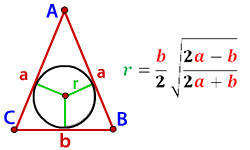
Заметим, что правильным многоугольником является выпуклый многоугольник, у которой равны как все стороны, так и все углы. Правильные многоугольники отличаются количеством углов и сторон. Точка, равноудаленная от вершин многоугольника и его сторон, называется центром такого многоугольника. В него можно легко вписать окружность. При этом стороны многоугольника будут касательными к окружности. Соответственно, вписанной в многоугольник окружностью считается окружность, касающаяся всех его сторон. Центры правильного многоугольника и вписанной в него окружности совпадают. Радиусом вписанного круга является апофема многоугольника или перпендикуляр, проведенный из центра на сторону многоугольника.
Для вычисления радиуса вписанного круга в правильный многоугольник, используем формулу:
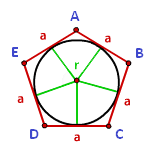
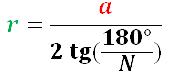
r — величина радиуса;
a — величина стороны;
n — количество сторон.
Чтобы быстро и правильно рассчитать r вписанной окружности, воспользуйтесь онлайн калькулятором.
