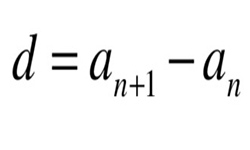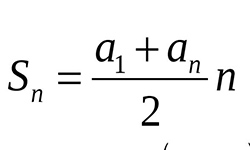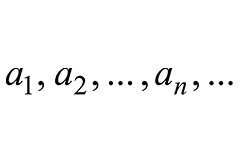Бесконечная последовательность чисел {bn}, каждое из которых, начиная со второго, можно найти путем умножения предыдущего на постоянное для этой последовательности число (q) не равное нулю, называется геометрической прогрессией. Т.е. bn+1 = bn×q, для любого натурального значения n = 2,3,... ; b1 = b. В геометрической прогрессии первый член {b1} не равен 0. Число q — знаменатель данной геометрической прогрессии.
Если знаменатель прогрессии (q) больше нуля, знак всех членов геометрической прогрессии совпадет со знаком заданного числа b.
Если знаменатель (q) меньше нуля, знаки у членов геометрической прогрессии будут чередоваться.
Если знаменатель (q) меньше 1, но больше -1, такая прогрессия будет бесконечно убывающей.
Рассчитать знаменатель геометрической прогрессии можно по формуле:
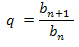Быстро рассчитать первые члены геометрической прогрессии можно с помощью онлайн калькулятора, указав известный член прогрессии, знаменатель и количество ее членов (n).
