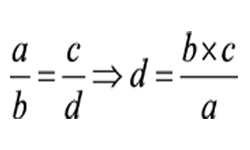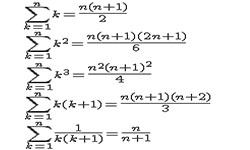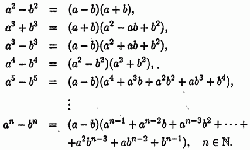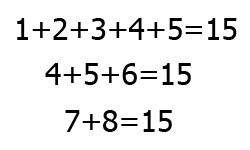Тройное правило используют при решении задач, в которых величины связаны между собой прямой или обратной пропорциональной зависимостью. В таких задачах имеются две величины, имеющие пропорциональную зависимость. При этом известны два значения одной величины (a1, a2) и одно значение другой (b1), второе значение которой (b2) необходимо найти. Прямую пропорциональность можно выразить …
Читать далее »Треугольник Паскаля
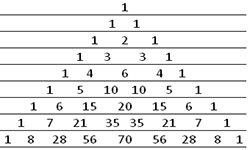
Известно, что числовой треугольник, по краям каждой строки которого стоят единицы, а всякое из остальных чисел равняется сумме 2-х стоящих над ним слева и справа чисел предыдущей строки, называется треугольником Паскаля. Придерживаясь этого правила, несложно выписывать друг за другом до бесконечности новые строки данного треугольника. Данный треугольник состоит из биномиальных …
Читать далее »Объединение множеств
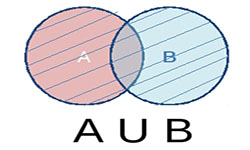
Известно, что объединением множеств А и В будет считаться множество С, при условии, что оно содержит все элементы хотя бы одного из множеств А или В, либо одновременно А и В. Символами «U» и «+» обозначается объединение множеств, в письменном виде его можно выразить таким образом: C = A U …
Читать далее »Разность множеств
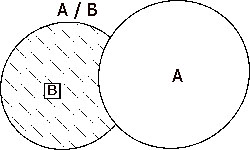
Два множества будут считаться равными, если они полностью состоят из одинаковых элементов. Это означает, что любой элемент одного множества принадлежит другому множеству и наоборот. Если в одном из множеств имеется хоть один элемент, не принадлежащий второму, данные множества не равные. Разностью между одним множеством А и другим множеством В будет …
Читать далее »Сумма последовательности
Формулы последовательностей: где k — порядковый номер; n — количество членов. Рассмотрим варианты быстрого нахождения суммы разного количества последовательных чисел. 1 вариант. Для того, чтобы определить сумму 5-ти последовательных чисел, следует умножить на 5 число, находящее посередине: (х — 2) + (х — 1) + (х) + (х + 1) + (х + 2) …
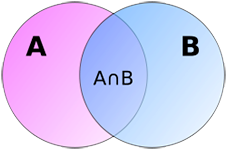
Читать далее »Пересечение множеств
Известно, что пересечением множеств А и В будет множество С, включающее общие элементы, принадлежащие одновременно как множеству А, так и множеству В. Если же у множеств А и В нет общих элементов, они являются не пересекающимися. Символами «∩» и «•» обозначается пересечение множеств, которое можно записать так: С = А …
Читать далее »Разложение на множители
Натуральные числа делятся на простые и составные. Различие между ними заключается в числе делителей. Простое число возможно разложить на него самого и 1. Например, 2, 5, 13, 23 ... Единица не считается простым числом. Число, которое раскладывается на более чем два делителя, называется составным. Любое составное число возможно представить как …
Читать далее »Последовательное число
Одним из важнейших понятий математики является последовательность, которая составляется из точек, чисел, векторов, функций и т.д. Чаще всего разбираются числовые последовательности, их членами являются числа. Для натуральных чисел последовательным будет число, которое на 1 больше, чем предыдущее. Например, в ряду 0 1 2 3 4 5 6 каждая последующая цифра …
Читать далее »Подмножество из множества
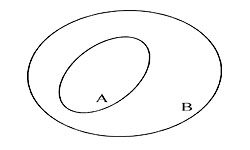
Множество представляет определенную совокупность объектов, которые называются элементами множества. Обозначаются множества заглавными латинскими буквами (А, В, С, X...), строчными латинскими а, b, c, x ... записывают элементы множества. Множество А считается подмножеством множества В, при условии, что все элементы множества А имеются во множестве В. Если в множестве не имеется …
Читать далее »Определить является ли число иррациональным
Как известно, рациональное число возможно выразить обыкновенной дробью. Это относится и к целым числам, и к конечным десятичным и к бесконечным периодическим десятичным дробям. Бесконечные непериодические десятичные дроби невозможно выразить обыкновенными дробями, это — иррациональные числа. Числа, которые не относятся к рациональным, т.е. ни целые, ни дробные вида m/n (m — целое …
Читать далее » Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач