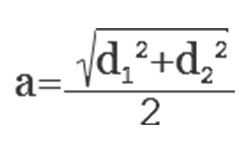Боковое ребро параллелепипеда

Четырехугольная призма, в основании которой находится параллелограмм, является параллелепипедом. В параллелепипеде 6 граней: 4 — боковые и 2 — его основание. Грани, как правило, представляют собой параллелограмм. Противолежащие грани параллельны и равны. Параллелепипеды бывают прямыми и наклонными. У прямого параллелепипеда боковые грани являются прямоугольниками. Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным. У него все шесть граней — прямоугольники, противоположные стороны которых параллельны и равны, а все углы — прямые. Прямоугольный параллелепипед строится на трех ребрах, расположенных друг к другу под прямым углом. Длины этих ребер, обладающих общим концом, называются его измерениями.

Боковое ребро прямоугольного параллелепипеда можно рассчитать несколькими способами, в зависимости от исходных данных.
Если известны объем (V) и два ребра (b, c) правильного параллелепипеда, третье ребро (а) будет равно частному от деления объема на произведение двух ребер (b×c):

a = V / bc

Если известна площадь боковой поверхности и два ребра (b, c), находим неизвестное ребро (а) путем деления площади боковой поверхности (S) на удвоенную сумму двух известных ребер 2 (b+c).

a = S_б.п. / 2 (a+c)

Если известны два ребра (b, c) и полная площадь поверхности (S п.п.), неизвестное ребро (а) находим по формуле:

a = (S_п.п. — 2bc) / 2 (b+c)

Проведенный внутри параллелепипеда отрезок, соединяющий противоположные вершины двух его оснований, является диагональю параллелепипеда (D). Отрезок, соединяющий противоположные вершины одного из оснований, является диагональю основания (d). Внутри прямоугольного параллелепипеда можно построить прямоугольный треугольник, у которого гипотенузой будет диагональ параллелепипеда D, одним из катетов — диагональ основания d, другим — боковое ребро параллелепипеда (а). Используя теорему Пифагора, выразим квадрат диагонали основания d (гипотенузу) как сумму квадратов его сторон (катетов) b, с. Отсюда, квадрат длины диагонали прямоугольного параллелепипеда (D) равен сумме квадратов трёх его измерений (а,b,с). Зная ребра и диагональ параллелепипеда, находим боковое ребро по формуле:

a = √D² + d² = √D² + b² + c²

где b, c — ребра параллелепипеда, a — боковое ребро параллелепипеда, D — диагональ параллелепипеда, d — диагональ основания.

Калькулятор расчета длины бокового ребра правильного параллелепипеда