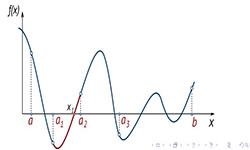
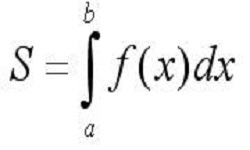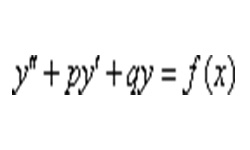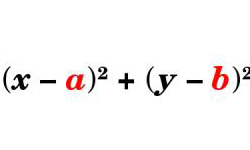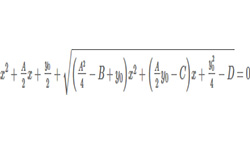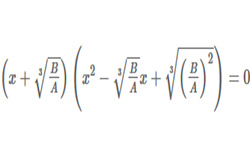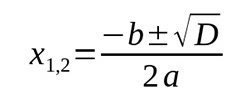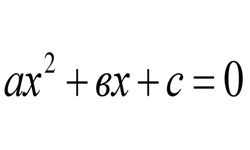Интегрирование или решение интегралов — операция, обратная дифференцированию. Геометрический смысл интеграла для функции у = f (х) — это площадь криволинейной трапеции. Решение определенного интеграла предполагает поиск значения функции в заданных пределах. Если интеграл неопределенный (нет границ интегрирования), решение предполагает нахождение первообразной: ʃ – значок интеграла; dх — значок дифференциала; f (х) — подынтегральная …

Равенство, содержащее лишь одну переменную исключительно в первой степени, представляет собой линейное уравнение. Такое уравнение имеет вид: ах + b = 0, где а, b — коэффициенты, х -переменная. Уравнения, которые путем равносильных преобразований можно привести к виду ах + b = 0, называют уравнениями, сводящимися к линейным уравнениям. Решение линейных …

Уравнение вида: a•xn + b•xn-1 + c•x2 + d•x + e = 0 называется полиномиальным уравнением n-й степени. Квадратное уравнение вида ах2 + bx + c = 0 представляет собой простейшее полиномиальное уравнение 2-й степени. Чтобы решить это уравнение, необходимо вычислить его корни по формуле: x = (- b ± …

Уравнение вида f (x) = 0, где f (x) — некая нелинейная функция, называется нелинейным. Виды таких уравнений: алгебраические, где функция алгебраическая, и трансцендентные, в которых функция может быть тригонометрическая, показательная и т.д. При решении нелинейных уравнений используются прямые (точные) и итерационные (численные) методы. Решить точным методом — значит, представить решение в …

В дифференциальных уравнениях (ДУ) второго порядка обязательно есть вторая производная у'', но отсутствуют производные высших порядков. Различают два типа линейных дифференциальных уравнений (ДУ) 2-го порядка с постоянными коэффициентами: однородные и неоднородные. Однородное ДУ имеет вид: у'' + ру' + qу = 0. В правой части уравнения всегда будет 0, р, …

Окружность — геометрическое место расположения множества точек, каждая из которых равноудалена от центра окружности. Отрезок, соединяющий любую точку окружности с ее центром, называется радиусом окружности. Величина радиуса равняется половине диаметра — отрезку, который соединяет две точки окружности, проходя через точку ее центра. Если в координатную плоскость поместить окружность с радиусом R и …

Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех значений неизвестного (неизвестных), при которых соблюдается верное равенство. Такие значения неизвестного (неизвестных) являются корнями или решением уравнения. Уравнение вида ах4 + bх3 + сх2 + dх + е = 0 называется уравнением 4-й степени с одним …

Уравнение представляет собой равенство, содержащее букву, значение которой нужно найти. Для обозначение неизвестных чисел наиболее часто пользуются буквами х, у, z. Кубическое уравнение — уравнение 3-го порядка вида: ax3 + bx2 + cx + d = 0, где a не равно 0. Решить уравнение означает найти такие значения числа х, подстановка …

Чтобы решить квадратное уравнение а2 + bх + с = 0, нужно вычислить дискриминант многочлена. Дискриминант (D) равен: D = b2 — 4ac. Определить количество корней в уравнении можно по знаку дискриминанта: если D больше 0, уравнение имеет два разных вещественных корня; если D меньше 0, уравнение имеет два корня, которые …

Равенство с неизвестными числами, которые нужно найти, называется уравнением. Обозначаются неизвестные чаще всего буквами х, у, z. Решить уравнение — это определить все его корни, которые являются значениями неизвестных, при которых уравнение становится числовым равенством. Уравнения, имеющие одинаковые корни, считаются равносильными. Чаще всего в математической практике нужно решать квадратные уравнения. Уравнения …