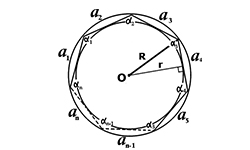
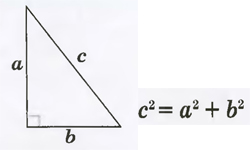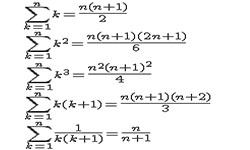Многоугольник представляет плоскую замкнутую геометрическую фигуру, у которой может быть три, четыре и более сторон, пересекающихся в трех, четырех и более точках, называющихся вершинами. Называются они в соответствии с количеством сторон или вершин. Например, многоугольник с пятью сторонами называется пятиугольник, с шестью — шестиугольник и т. д. Правильным называют многоугольник с …
Читать далее »nikto31
Теорема Пифагора
Теорема Пифагора — главное утверждение геометрии. Так звучит ее формулировка : площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. S = S1 + S2 Несмотря на то, что теорема названа именем знаменитого математика и философа Пифагора, проживавшего в Древней Греции в VI в. до …
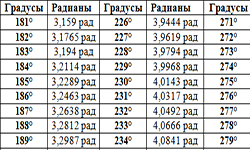
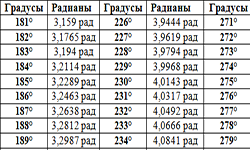
Читать далее »Таблица синусов
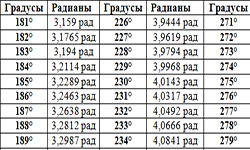
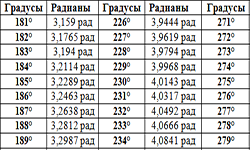
Таблица Брадиса. Она содержит рассчитанные значения синусов, косинусов, тангенсов и котангенсов углов, начиная с 0° до 360°. Воспользовавшись таблицей тригонометрических функций, можно производить расчеты и без инженерного калькулятора. В таблице можно легко найти значение тригонометрических функций от заданного Вам угла. Таблица синусов. Как известно, прямоугольный треугольник имеет три угла, два …
Читать далее »Таблица косинусов
Косинусом острого угла считается отношение величины прилежащего катета к величине гипотенузы. Прилежащим является катет, расположенный на одной из сторон угла. cos (A) = в / с где в — прилежащий катет; с — гипотенуза. Косинус является тригонометрической функцией угла. Если нам известна величина угла, мы можем определить косинус угла, воспользовавшись таблицей Брадиса. …
Читать далее »Таблица тангенсов
Современные определения тригонометрических функций и их символика принадлежат Л. Эйлеру. Хотя еще в 3-м в. до н. э в трудах Архимеда, Евклида и других рассматриваются отношения сторон в прямоугольном треугольнике, что фактически и является тригонометрическими функциями. В переводе с греческого тригонометрия означает «треугольник» и «измеряю» и является разделом математики, изучающим …
Читать далее »Таблица котангенсов
Тригонометрия является разделом математики, в которой рассматривается зависимость между сторонами треугольника и углами. Как известно, в прямоугольном треугольнике один угол обязательно прямой, остальные острые. Стороны, прилежащие к углу в 90 градусов, являются катетами треугольника, а сторона, расположенная против прямого угла, — его гипотенуза. Соотношения двух сторон прямоугольного треугольника представляют собой тригонометрические …
Читать далее »Треугольник Паскаля
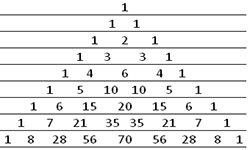
Известно, что числовой треугольник, по краям каждой строки которого стоят единицы, а всякое из остальных чисел равняется сумме 2-х стоящих над ним слева и справа чисел предыдущей строки, называется треугольником Паскаля. Придерживаясь этого правила, несложно выписывать друг за другом до бесконечности новые строки данного треугольника. Данный треугольник состоит из биномиальных …
Читать далее »Объединение множеств
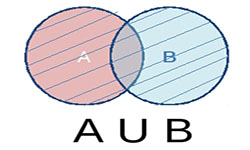
Известно, что объединением множеств А и В будет считаться множество С, при условии, что оно содержит все элементы хотя бы одного из множеств А или В, либо одновременно А и В. Символами «U» и «+» обозначается объединение множеств, в письменном виде его можно выразить таким образом: C = A U …
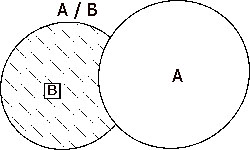
Читать далее »Разность множеств
Два множества будут считаться равными, если они полностью состоят из одинаковых элементов. Это означает, что любой элемент одного множества принадлежит другому множеству и наоборот. Если в одном из множеств имеется хоть один элемент, не принадлежащий второму, данные множества не равные. Разностью между одним множеством А и другим множеством В будет …
Читать далее »Сумма последовательности
Формулы последовательностей: где k — порядковый номер; n — количество членов. Рассмотрим варианты быстрого нахождения суммы разного количества последовательных чисел. 1 вариант. Для того, чтобы определить сумму 5-ти последовательных чисел, следует умножить на 5 число, находящее посередине: (х — 2) + (х — 1) + (х) + (х + 1) + (х + 2) …
Читать далее » Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач
Помощник в обучении Сайт помощник в обучении. Онлайн калькуляторы, тренажеры и справочники для решения и выполнения математических и других видов задач